Introdução à Matriz: Explorando a Linguagem dos Números e Relações

Seja bem-vindo ao fascinante mundo das matrizes! Neste tópico, vamos mergulhar na compreensão das matrizes, que são essenciais para diversas áreas da matemática, ciência da computação, engenharia e muito mais. Prepare-se para explorar a linguagem dos números e suas relações de uma maneira totalmente nova e emocionante.

1. Definição de Matriz:

Uma matriz é uma estrutura organizada de números ou elementos dispostos em linhas e colunas. Ela é representada entre colchetes ou parênteses e pode assumir diferentes formas e tamanhos. Por exemplo:

$�=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$

Nesta matriz $�$, temos 2 linhas e 3 colunas, e os números individuais são chamados de elementos da matriz.

2. Tipos de Matrizes:

Existem diversos tipos de matrizes, cada uma com suas características específicas:

• Matriz Linha: Uma matriz com apenas uma linha.
• Matriz Coluna: Uma matriz com apenas uma coluna.
• Matriz Quadrada: Uma matriz com o mesmo número de linhas e colunas.
• Matriz Retangular: Uma matriz com um número diferente de linhas e colunas.
• Matriz Nula: Uma matriz em que todos os elementos são zero.
• Matriz Diagonal: Uma matriz em que todos os elementos fora da diagonal principal são zero.

1. Matriz Linha: Uma matriz linha é aquela que possui apenas uma linha. Por exemplo: $�=\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$ Neste exemplo, a matriz $�$ é uma matriz linha com os elementos 1, 2 e 3.

2. Matriz Coluna: Uma matriz coluna é aquela que possui apenas uma coluna. Por exemplo: $�=\left[\begin{array}{c}4\\ 5\\ 6\end{array}\right]$ Neste caso, a matriz $�$ é uma matriz coluna com os elementos 4, 5 e 6.

3. Matriz Quadrada: Uma matriz quadrada tem o mesmo número de linhas e colunas. Por exemplo: $�=\left[\begin{array}{cc}2& 3\\ 4& 5\end{array}\right]$ A matriz $�$ é uma matriz quadrada de ordem 2, pois possui 2 linhas e 2 colunas.

4. Matriz Retangular: Uma matriz retangular tem um número diferente de linhas e colunas. Por exemplo: $�=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$ A matriz $�$ é uma matriz retangular com 2 linhas e 3 colunas.

5. Matriz Nula: Uma matriz nula é aquela em que todos os elementos são zero. Por exemplo: $�=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$ A matriz $�$ é uma matriz nula de ordem 2, pois possui 2 linhas e 2 colunas.

6. Matriz Diagonal: Uma matriz diagonal é aquela em que todos os elementos fora da diagonal principal são zero. Por exemplo: $�=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right]$ A matriz $�$ é uma matriz diagonal com os valores próprios 1, 2 e 3 na diagonal principal.

• 
  
  
  
  

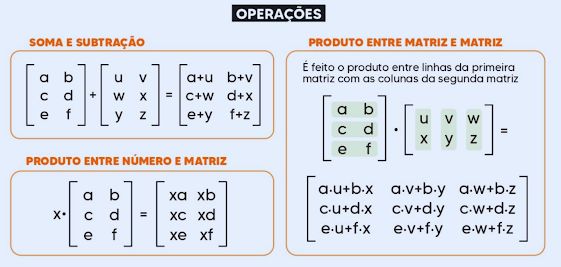
3. Operações Básicas com Matrizes:

As operações básicas com matrizes incluem adição, subtração e multiplicação por um escalar:

• Adição de Matrizes: A adição é realizada somando os elementos correspondentes das matrizes.
• Subtração de Matrizes: A subtração é realizada subtraindo os elementos correspondentes das matrizes.
• Multiplicação por Escalar: Multiplica cada elemento da matriz por um número escalar.

Por exemplo, se tivermos as matrizes:

$�=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$ $�=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]$

A adição de matrizes $�+�$ resultaria em:

$�+�=\left[\begin{array}{cc}1+5& 2+6\\ 3+7& 4+8\end{array}\right]=\left[\begin{array}{cc}6& 8\\ 10& 12\end{array}\right]$

4. Propriedades Básicas das Operações com Matrizes:

As operações com matrizes têm propriedades interessantes, como associatividade, comutatividade e distributividade. Por exemplo:

• A adição de matrizes é associativa: $(�+�)+�=�+(�+�)$
• A multiplicação de matrizes é distributiva: $�(�+�)=��+��$
• A multiplicação de matrizes não é comutativa: $��\mathrm{\ne }��$

Explorar essas propriedades nos ajuda a entender melhor as relações entre as matrizes e a aplicar esse conhecimento em uma variedade de situações práticas.

Neste tópico, mergulhamos na definição, tipos, operações básicas e propriedades das matrizes. Agora, com uma compreensão sólida desses fundamentos, estamos preparados para avançar para conceitos mais avançados e aplicações empolgantes das matrizes em nossas jornadas matemáticas e científicas.

Operações Avançadas com Matrizes: Desvendando os Segredos da Manipulação Matricial

Bem-vindo ao universo das operações avançadas com matrizes, onde exploramos os intricados meandros da multiplicação, inversão e decomposição. Prepare-se para mergulhar em conceitos complexos, mas poderosos, que são fundamentais em uma variedade de disciplinas, desde álgebra linear até ciência da computação e engenharia.

1. Multiplicação de Matrizes:

A multiplicação de matrizes é uma operação fundamental que permite combinar informações de diferentes maneiras. Seja $�$ uma matriz $�\times �$ e $�$ uma matriz $�\times �$, o produto $��$ é uma matriz $�\times �$. O elemento $(�,�)$ de $��$ é calculado multiplicando os elementos da $�$-ésima linha de $�$ pelos elementos da $�$-ésima coluna de $�$ e somando os resultados.

$(��{)}_{��}={\sum }_{�=1}^{�}(�{)}_{��}\times (�{)}_{��}$

2. Matriz Identidade e Inversa:

Uma matriz identidade, denotada por $�$, é uma matriz quadrada em que todos os elementos da diagonal principal são 1 e todos os outros elementos são 0. Para qualquer matriz quadrada $�$ de ordem $�$, temos $��=�$ e $��=�$. Uma matriz inversa de $�$, denotada por ${�}^{-1}$, é aquela em que $�{�}^{-1}={�}^{-1}�=�$. Nem todas as matrizes têm uma inversa.

3. Determinante de uma Matriz:

O determinante de uma matriz quadrada é um número especial que fornece informações importantes sobre a matriz. Ele é denotado por $\mathrm{\mid }�\mathrm{\mid }$. O determinante de uma matriz $2\times 2$ é calculado pela fórmula $\mathrm{\mid }�\mathrm{\mid }=��-��$, onde $�=\left[\begin{array}{cc}�& �\\ �& �\end{array}\right]$. Para matrizes maiores, existem várias regras e métodos para calcular o determinante.

4. Sistemas de Equações Lineares:

Matrizes são amplamente utilizadas para resolver sistemas de equações lineares. Se tivermos um sistema de equações lineares na forma $��=�$, onde $�$ é uma matriz de coeficientes, $�$ é o vetor de incógnitas e $�$ é o vetor de constantes, podemos resolver o sistema multiplicando ambos os lados por ${�}^{-1}$, desde que $�$ seja inversível.

5. Propriedades e Aplicações:

As operações avançadas com matrizes têm muitas propriedades interessantes e são fundamentais em muitas áreas. Elas são amplamente utilizadas em computação gráfica, processamento de imagens, redes neurais, física, estatística e muito mais. A compreensão dessas operações permite resolver problemas complexos e modelar uma variedade de fenômenos do mundo real.

Neste tópico, exploramos as operações avançadas com matrizes, incluindo multiplicação, inversão, determinante e aplicação em sistemas de equações lineares. Com um entendimento sólido desses conceitos, estamos preparados para enfrentar desafios mais complexos e empolgantes em nossa jornada pelo mundo matricial.

Espaço Vetorial e Transformações Lineares: Explorando a Geometria das Matrizes

Bem-vindo a uma jornada fascinante pelo mundo dos espaços vetoriais e transformações lineares! Neste tópico, vamos explorar as profundezas da geometria das matrizes, revelando padrões, relações e aplicações surpreendentes que permeiam essa área crucial da álgebra linear.

1. Espaço Vetorial:

Um espaço vetorial é uma estrutura matemática que consiste em um conjunto de elementos chamados vetores, juntamente com duas operações, adição de vetores e multiplicação por um escalar. Para ser um espaço vetorial, o conjunto deve satisfazer uma série de propriedades, incluindo fechamento sob as operações, associatividade, existência de vetor nulo e inverso aditivo, entre outros.

2. Subespaços Vetoriais:

Um subespaço vetorial é um subconjunto de um espaço vetorial que é fechado sob as operações de adição de vetores e multiplicação por um escalar. Isso significa que os vetores dentro do subespaço permanecem no subespaço quando adicionados ou multiplicados por um escalar. Subespaços vetoriais são essenciais para entender a estrutura e as propriedades dos espaços vetoriais.

3. Transformações Lineares:

Uma transformação linear é uma função entre dois espaços vetoriais que preserva a estrutura vetorial, ou seja, preserva a adição de vetores e a multiplicação por escalares. Uma transformação linear é representada por uma matriz, e seu comportamento pode ser visualizado geometricamente por meio da transformação dos vetores de entrada.

4. Núcleo e Imagem de uma Transformação Linear:

O núcleo (ou kernel) de uma transformação linear é o conjunto de todos os vetores de entrada que são mapeados para o vetor nulo. A imagem de uma transformação linear é o conjunto de todos os vetores de saída que são obtidos a partir da aplicação da transformação aos vetores de entrada. Esses conceitos são fundamentais para entender a estrutura e o comportamento das transformações lineares.

5. Isomorfismo entre Espaços Vetoriais:

Dois espaços vetoriais são ditos isomorfos se houver uma correspondência biunívoca entre eles que preserve a estrutura vetorial. Isso significa que os dois espaços têm a mesma estrutura matemática, embora possam ter diferentes representações. O isomorfismo é uma ferramenta poderosa para comparar e entender espaços vetoriais de maneira mais profunda.

Neste tópico, mergulhamos nas profundezas do espaço vetorial e das transformações lineares, revelando a intrincada geometria e estrutura por trás desses conceitos fundamentais. Com uma compreensão sólida desses temas, estamos preparados para explorar aplicações avançadas em áreas como álgebra, geometria, física e engenharia.

Decomposições Especiais de Matrizes: Desvendando os Segredos da Estrutura Matricial

Bem-vindo a um mundo de decomposições matriciais especiais, onde exploramos as técnicas sofisticadas e poderosas para desvendar a estrutura interna das matrizes. Prepare-se para uma jornada emocionante enquanto mergulhamos nas profundezas das decomposições LU, Cholesky, QR e SVD, revelando seus segredos e aplicações surpreendentes.

1. Decomposição LU (Lower-Upper):

A decomposição LU é uma técnica que fatora uma matriz em dois componentes: uma matriz triangular inferior (L) e uma matriz triangular superior (U). Essa decomposição é frequentemente usada para resolver sistemas de equações lineares e encontrar inversas de matrizes. A decomposição LU é uma ferramenta poderosa para simplificar cálculos e resolver problemas complexos de forma eficiente.

2. Decomposição de Cholesky:

A decomposição de Cholesky é uma decomposição especial de uma matriz simétrica e definida positiva em um produto de uma matriz triangular inferior e sua transposta conjugada. Essa decomposição é especialmente útil em problemas envolvendo sistemas de equações lineares, otimização quadrática e simulação estocástica. A decomposição de Cholesky permite uma representação mais compacta e eficiente de matrizes simétricas.

3. Decomposição QR:

A decomposição QR fatora uma matriz em um produto de uma matriz ortogonal (Q) e uma matriz triangular superior (R). Essa decomposição é amplamente utilizada em problemas de regressão linear, mínimos quadrados, ajuste de curvas e determinação de autovalores e autovetores. A decomposição QR é uma ferramenta poderosa para encontrar soluções aproximadas e estáveis para uma variedade de problemas.

4. Decomposição em Valores Singulares (SVD):

A decomposição em valores singulares é uma técnica que fatora uma matriz em três componentes: uma matriz unitária esquerda, uma matriz diagonal de valores singulares e uma matriz unitária direita. Essa decomposição é fundamental em análise de componentes principais, redução de dimensionalidade, processamento de sinais e reconhecimento de padrões. A decomposição SVD é uma ferramenta versátil e poderosa para análise e modelagem de dados.

5. Aplicações e Significado:

As decomposições especiais de matrizes têm uma ampla gama de aplicações em diversas áreas, incluindo matemática, ciência da computação, física, engenharia e muito mais. Essas técnicas são essenciais para resolver problemas complexos, modelar fenômenos do mundo real e fazer previsões precisas. Ao compreender as decomposições de matrizes, somos capazes de explorar as estruturas subjacentes dos dados e obter insights valiosos.

Neste tópico, exploramos as decomposições especiais de matrizes, revelando sua importância, aplicações e significado em uma variedade de contextos. Compreender essas técnicas nos capacita a resolver problemas desafiadores e aproveitar ao máximo o poder das matrizes em nossas análises e modelagens.

Aplicações de Matrizes na Ciência da Computação: Construindo Pontes entre a Teoria e a Prática

Bem-vindo a um universo onde as matrizes se tornam as ferramentas essenciais na resolução de problemas computacionais complexos e na construção de sistemas inteligentes. Neste tópico, vamos explorar as diversas maneiras pelas quais as matrizes são aplicadas na ciência da computação, revelando sua importância e impacto em uma ampla gama de áreas e tecnologias.

1. Grafos e Representação de Grafos:

As matrizes são amplamente utilizadas na representação e análise de grafos, que são estruturas de dados fundamentais na ciência da computação. A matriz de adjacência é uma das formas mais comuns de representar grafos em matrizes, onde cada entrada indica se há uma aresta entre dois vértices. Essa representação permite uma análise eficiente de propriedades e algoritmos de grafos.

2. Algoritmos de Busca de Caminho Mínimo:

Algoritmos como o algoritmo de Dijkstra e o algoritmo de Bellman-Ford, usados para encontrar o caminho mínimo em um grafo ponderado, frequentemente fazem uso de matrizes para armazenar e manipular informações sobre distâncias entre vértices. Esses algoritmos têm uma ampla gama de aplicações em redes de computadores, sistemas de navegação e logística.

3. Redes Neurais e Aprendizado de Máquina:

As matrizes desempenham um papel fundamental no funcionamento de redes neurais artificiais e algoritmos de aprendizado de máquina. As entradas, pesos, bias e saídas das redes neurais são representados e manipulados como matrizes, permitindo o treinamento e a inferência eficientes em conjuntos de dados complexos.

4. Processamento de Imagens e Reconhecimento de Padrões:

Em aplicações de processamento de imagens e reconhecimento de padrões, as imagens são frequentemente representadas como matrizes de pixels. Técnicas de filtragem, segmentação e reconhecimento são implementadas usando operações matriciais para extrair características e informações úteis das imagens.

5. Outras Aplicações:

Além disso, as matrizes são amplamente aplicadas em áreas como processamento de sinais, criptografia, compressão de dados, simulação, modelagem e muito mais. Sua versatilidade e poder computacional fazem delas uma ferramenta indispensável na resolução de uma ampla variedade de problemas computacionais.

Neste tópico, exploramos as diversas maneiras pelas quais as matrizes são aplicadas na ciência da computação, revelando seu papel essencial na resolução de problemas complexos e na construção de sistemas inteligentes. Compreender essas aplicações nos capacita a aproveitar ao máximo o potencial das matrizes em nossas jornadas tecnológicas e científicas.

Aqui estão algumas das fórmulas mais comuns utilizadas no conteúdo de matrizes:

1. Multiplicação de Matrizes: $(��{)}_{��}={\sum }_{�=1}^{�}(�{)}_{��}\times (�{)}_{��}$

2. Matriz Identidade:

3. Determinante de uma Matriz $2\times 2$: $\mathrm{\mid }�\mathrm{\mid }=��-��$

4. Determinante de uma Matriz $3\times 3$: $\mathrm{\mid }�\mathrm{\mid }=�(��-�ℎ)-�(��-��)+�(�ℎ-��)$

5. Soma dos Elementos de uma Matriz: ${\sum }_{�=1}^{�}{\sum }_{�=1}^{�}{�}_{��}$

6. Inversa de uma Matriz: Se ${�}^{-1}$ existe, então $�{�}^{-1}={�}^{-1}�=�$

7. Transposição de uma Matriz: Se $�={�}^{�}$, então ${�}_{��}={�}_{��}$

8. Multiplicação de uma Matriz por um Escalar: Se $�=��$, então ${�}_{��}=�{�}_{��}$

9. Traço de uma Matriz Quadrada: $\text{tr}(�)={\sum }_{�=1}^{�}{�}_{��}$

10. Decomposição LU: Se $�=��$, onde $�$ é uma matriz triangular inferior e $�$ é uma matriz triangular superior.

11. Decomposição QR: Se $�=��$, onde $�$ é uma matriz ortogonal e $�$ é uma matriz triangular superior.

12. Decomposição SVD (Valores Singulares): Se $�=�\mathrm{\Sigma }{�}^{�}$, onde $�$ e $�$ são matrizes ortogonais e $\mathrm{\Sigma }$ é uma matriz diagonal com valores singulares.

Essas são apenas algumas das fórmulas essenciais usadas no estudo de matrizes. Elas são fundamentais para a compreensão e aplicação de conceitos matriciais em uma variedade de campos, desde álgebra linear até processamento de sinais e aprendizado de máquina.

Fórmula	Descrição
$(��{)}_{��}={\sum }_{�=1}^{�}(�{)}_{��}\times (�{)}_{��}$	Multiplicação de Matrizes
[	A
[	A
${\sum }_{�=1}^{�}{\sum }_{�=1}^{�}{�}_{��}$	Soma dos Elementos de uma Matriz
Se ${�}^{-1}$ existe, então $�{�}^{-1}={�}^{-1}�=�$	Inversa de uma Matriz
Se $�={�}^{�}$, então ${�}_{��}={�}_{��}$	Transposição de uma Matriz
Se $�=��$, então ${�}_{��}=�{�}_{��}$	Multiplicação de uma Matriz por um Escalar
$\text{tr}(�)={\sum }_{�=1}^{�}{�}_{��}$	Traço de uma Matriz Quadrada
Se $�=��$, onde $�$ é uma matriz triangular inferior e $�$ é uma matriz triangular superior.	Decomposição LU
Se $�=��$, onde $�$ é uma matriz ortogonal e $�$ é uma matriz triangular superior.	Decomposição QR
Se $�=�\mathrm{\Sigma }{�}^{�}$, onde $�$ e $�$ são matrizes ortogonais e $\mathrm{\Sigma }$ é uma matriz diagonal com valores singulares.	Decomposição SVD (Valores Singulares)