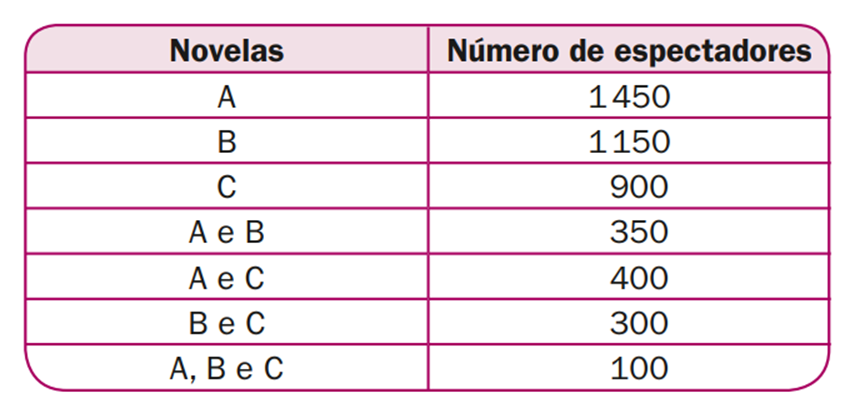
(U.E. Londrina-PR) Num dado momento, três canais de TV tinham, em sua programação, novelas em seus horários nobres: a novela A no canal A, a novela B no canal B e a novela C no canal C. Numa pesquisa com 3000 pessoas, perguntou-se quais novelas agradavam. A tabela a seguir indica o número de telespectadores que designaram as novelas como agradáveis.
Quantos telespectadores entrevistados não acham agradável nenhuma das três novelas? a) 300A quantidade de telespectadores entrevistados que não acham agradável nenhuma das três novelas é 450 espectadores.
A solução do problema proposto passa pela aplicação da teoria dos conjuntos, onde é muito útil o uso dos diagramas representativos conhecidos como diagrama de Venn.
Neste diagrama, você tem a possibilidade de visualizar os conjuntos e suas interseções e, deste modo, responder facilmente às questões apresentadas.
Vejamos, pelo enunciado:
- Temos três conjuntos: A, B e C;
- A interseção dos três conjuntos é: A, B e C = 100;
- A interseção de conjuntos dois a dois é: A e B = 350; A e C = 400; B e C = 300;
- A = 1450;
- B = 1150;
- C = 900.
Para operacionalizar a construção do diagrama, seguimos os passos:
- Desenhamos os três conjuntos e suas interseções (círculos) dentro de um retângulo que representa o todo. Em seguida, rotulamos os conjuntos;
- Começamos pela inserção da interseção dos três conjuntos no seu local apropriado (ver figura);
- Preenchemos a interseção de dois conjuntos subtraindo das quantidades a interseção entre três conjuntos;
- Completamos com a quantia que cabe a somente um conjunto apenas, também descontando a interseção de dois e três conjuntos.
- Finalmente, subtraímos do todo a quantidade que cabe a algum conjunto e esta diferença representa aquele que não participa de nenhum.
Observando o diagrama, temos que a quantidade de telespectadores entrevistados que não acham agradável nenhuma das três novelas é 450 espectadores.