Desvendando os Mistérios da Função Composta: Uma Viagem pelo Mundo da Matemática

Introdução:

A matemática é como um quebra-cabeça fascinante, cheio de peças interconectadas que formam um todo coeso. Entre essas peças, a função composta destaca-se como uma ferramenta poderosa para entender as relações entre diferentes funções. Neste artigo, exploraremos os conceitos fundamentais da função composta, sua aplicação prática e como ela nos permite desvendar enigmas matemáticos de forma elegante e eficiente.

O que é uma Função Composta?

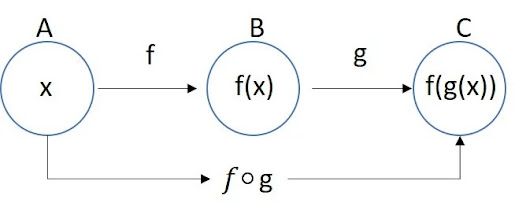
Uma função composta é o resultado da combinação de duas ou mais funções para formar uma nova função. Se tivermos duas funções, $�(�)$ e $�(�)$, a função composta, denotada por $(�\circ �)(�)$, é obtida ao aplicar primeiro $�$ a $�$ e depois aplicar $�$

f ao resultado. Matematicamente, isso é expresso como:

(f∘g)(x)=f(g(x))

Entendendo a Notação:

A notação $(�\circ �)(�)$ pode parecer complexa à primeira vista, mas ela simplifica a composição de funções. Imagine $�$ como uma máquina que transforma entradas, e $�$ como outra máquina. A função composta $(�\circ �)(�)$ representa a operação de passar $�$ pela máquina $�$ e, em seguida, pegar o resultado e passá-lo pela máquina $�$.

Exemplos Práticos:

1. Função Linear e Quadrática: Considere $�(�)=2�$ e $�(�)={�}^2$. A função composta $(�\circ �)(�)$ seria $�(�(�))=�({�}^2)=2{�}^2$. Aqui, a saída da função quadrática $�(�)$ é usada como entrada para a função linear $�(�)$.

2. Funções Trigonométricas: Suponha $�(�)=\sin (�)$ e $�(�)=\cos (�)$. A função composta $(�\circ �)(�)$ seria $�(�(�))=\sin (\cos (�))$. Neste caso, estamos combinando funções trigonométricas para criar uma nova função.

Propriedades Importantes:

1. Associatividade: A composição de funções é associativa, ou seja, $(�\circ �)\circ ℎ=�\circ (�\circ ℎ)$. Isso significa que a ordem em que as funções são compostas não altera o resultado final.

2. Identidade: Existe uma função identidade, denotada por $�(�)=�$, que não altera o valor de $�$. Para qualquer função $�(�)$, temos $(�\circ �)(�)=�(�)=(�\circ �)(�)$.

Aplicações na Vida Real:

A função composta não é apenas uma abstração matemática; ela tem aplicações práticas em várias áreas. Por exemplo, em física, as equações que descrevem o movimento de objetos muitas vezes envolvem funções compostas. Na economia, a modelagem de relações complexas entre variáveis também pode ser realizada por meio de funções compostas.

Conclusão:

A função composta é uma ferramenta valiosa que nos permite compreender e modelar relações matemáticas de maneira mais eficiente. À medida que exploramos esse conceito, percebemos como ele se estende por diferentes ramos da matemática e tem implicações práticas em nossa compreensão do mundo ao nosso redor. Ao dominar a arte da função composta, abrimos as portas para desvendar os mistérios matemáticos com confiança e precisão.